I’m pretty convinced modern AI will be a world-transforming technology. As such, I think it’s important that non-professionals understand how and why it works. My goal here is to explain to a broader audience — readers who don’t know calculus — how OpenAI’s DALL-E image generator works, in reasonably thorough and rigorous detail, with a few illustrative diagrams … but no math whatsoever. Wish me luck.
v. Let’s get noisy
As mentioned in Part 1 of this post, DALL-E is first taught how to add noise to pictures, and then to reverse that process and “denoise” from smeared static into clarity, from chaos into order. But what do we really mean when we say “noise?”
Think of static on an old-fashioned TV, or a noise machine for sleeping. Any such “messy” distribution of sounds or pixels is called noise. Which, it turns out, is a complex and subtle subject in and of itself. One particularly common kind of noise is called Gaussian, because its messiness is smeared across the audio or visual spectrum in the famous “bell curve” distribution first described by the great mathematician Carl Gauss. This noise is frequently found in nature. If you have a bad sensor, or a glitching electrical circuit, or you measure the Brownian motion in your coffee cup, you’ll probably get Gaussian noise. This is the noise used to train DALL-E, mostly because it’s mathematically convenient.
You don’t need a neural network to add noise to an image. We can calculate a relatively mathematically simple “noising process,” in which more and more noise is gradually added to an image, over perhaps a thousand steps, until the original is gone and all that’s left is pure noise. (This process is sometimes called “diffusion,” which is why DALL-E is often called a “diffusion model.”) This noise isn’t necessarily added at the same rate; e.g. you get better results if you add it more slowly at the beginning, when the image is cleanest. The chosen rate is known as the variance schedule, and like the learning rate, it too tends to be something of a judgement call.

Noising is pretty easy … but you cannot denoise with simple math. For that you need a fully trained neural network (often known as a “model,” an annoyingly generic word, but one used across the AI industry.) The secret key to DALL-E, the magic at its heart, is a model trained to look at a noisy image — a sample image taken from anywhere in a diffusion process — and estimate the noise added since the previous step in the process.
This is where the magic happens. Suppose the diffusion process with which you trained your model had 1,000 steps, invariably ending after the thousandth in pure Gaussian noise, seemingly incomprehensible random chaos. Well, if you show your trained model some of that pure noise … it has learned how to estimate the change since the step just before random chaos. You can then remove that estimated noise from the pure randomness, resulting in, in effect, the model’s estimate of a 999th step, a point at which where there is the tiniest hint of structure, the merest suggestion of some kind of order. So far, so little. To the human eye, that estimated 999th step will still be indistinguishable from chaos. But…
…then you run that estimated 999th step through the network again, to generate an estimated 998th step … and then a 997th … and very slowly, step by step, patterns begin to appear which seem non-random, and then, ultimately, recognizable to the human eye … forms, then shapes, then images, even faces … and eventually, after a thousand backwards steps, you wind up with a glorious, brand-new image, generated on the spot. Brand-new because, remember, the neural network estimates the added noise, rather than making precise calculations, so every input will lead to new estimation fuzziness at each step, and ultimately a different result.
In the end, as you’ve no doubt witnessed, the generated DALL-E image can be as photorealistic, as apparently seamless, as any of the original set of high-quality, human-generated images on which the diffusion model was initially trained. It feels like sorcery! But it’s really just a huge number of very repetitive, quite simple mathematical calculations … which accumulate into enormous power and subtlety.
OK, before we end this section, I can’t resist a little inside mathematical baseball. (Not that I’m a mathematician — I can barely even follow along re most of this stuff.) Initially, diffusion models were developed in parallel with a mathematically different kind of image-generation neural network known as score-based models. But after a few years of this, remarkably, it was established that both were different views of a single deeper, more fundamental method. To me the idea that we’re still very much actively exploring new theoretical territory, and making surprising discoveries about unexpectedly intersecting forms of neural computation, is goosebumps territory … but maybe to real mathematicians it seems a lot more prosaic.
v. It’s time to nudge
We’ve now seen how neural networks work in general, and how a diffusion model can generate an image by starting with randomness, and slowly reducing noise, until all that’s left is newly generated clarity. But of course DALL-E doesn’t generate random images. It takes a text prompt and turns it into something corresponding to that text, often even directly recognizable. How does that happen?
The trick is to add conditioning information at every step, i.e. to “nudge” the model slightly each time it estimates noise. This is called guided diffusion. If you saw Stranger Things, a good analogy is the Plinko board at the Hawkins Lab, pictured below.
The red disc falls randomly through the pins … but the psionically gifted, such as Eleven, can nudge the disc in the desired direction, right or left, each time it hits a pin, and ultimately guide it into a targeted slot at the bottom. This is a good metaphor for guided diffusion. The disc is the image being generated; each level of pins is a step in the denoising process; Eleven’s psychic powers are the nudges based on the text prompt; and the slot the disc falls into is the final image. (Although DALL-E boasts an effectively infinite number of final slots.)
But where does the guidance come from? It turns out you can train a diffusion model not just on images alone, but on images and their captions. If you run half your training runs with captions, and half without, you get a diffusion model which can take a text prompt and then, when denoising, add a new term to the estimation — the “nudge” — such that it denoises in the general direction of images vaguely like those whose captions had some commonality with your text prompt. The upshot is that the text prompt the user entered is compared to the captions on the images in the training set, and the resonance between them becomes a kind of faint magnetic influence on the denoising process, nudging the results towards the prompt.
This solution is known as “classifier-free” guided diffusion. Over time, it gets … well, actually, for DALL-E at least, pretty bad results. Neural networks are really hard to architect and optimize! But. It turns out that if you take another neural network, known as an “encoder,” trained on images and captions to recognize the connections between words and images; feed the user’s text prompt into the encoder; run its outputs into yet another diffusion model, known as the “prior”; and then connect its outputs to the inputs of your trained classifier-free diffusion model, called the “decoder” … then you get the glorious DALL-E outputs we know and love. That’s right, DALL-E isn’t one neural network, but three: encoder, prior, and decoder.
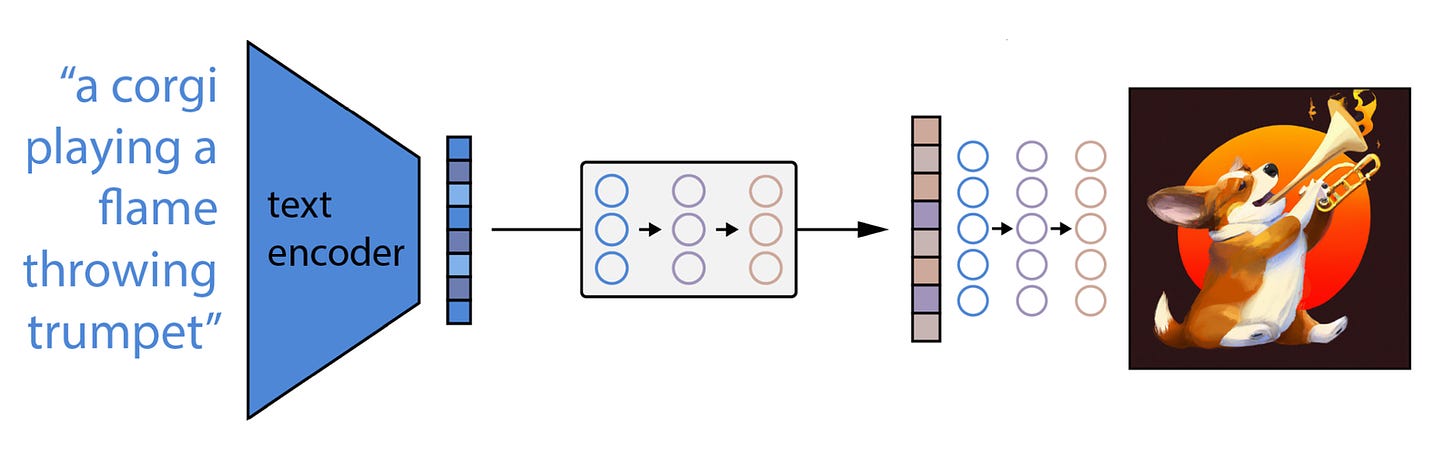
But when we talk about “outputs” of the encoder and prior, what exactly are we talking about? Formally, the encoder generates “text embeddings,” and the prior converts those to “image embeddings.” But what the heck is an embedding?
Well, one thing that happens when you train a neural network is that it slowly builds up its own representations of things. When we look at a painting, we can mentally break it down into its various components: faces, objects, shadows, generic shapes like curves and boxes, brightness, brush strokes, etc. Similarly, when you train a neural network on images or text, it learns to recognize elements that occur frequently, register them as common components, and then “see” new inputs as an assembly of those components. These are the embeddings. Not ones that humans would recognize, necessarily, but they become very efficient representations.
DALL-E’s chain of three models — user input to text embedding to image embedding to generated image — illustrates two important themes across modern AI:
a powerful model may have enormous potential capacities, but unlocking them with the right inputs can be almost as challenging as training it in the first place.
there is a lot of trial, error, judgement, and sometimes guesswork involved in stacking layers within neural networks, connecting those layers, determining parameters like learning rate and variance schedule, and then, when you have fully trained models, stacking them together to get the best results. It’s like AI research has given (and is giving) us a huge pile of new Lego blocks, which, if connected in the right ways, can construct genuinely extraordinary machinery capable of previously undreamt-of feats … but they still come with very limited and often completely baffling instructions.
vi. Skip connect the U-Net, then up the down sample
Let’s dig a little deeper into the neural networks which make up DALL-E’s engine. We previously mentioned that a neural network is made up of many “layers.” Well, just as there are many different kinds of neural networks, there are many different kinds of layers comprising each network. Again, think of layers as Lego blocks, and neural networks as Lego creations made up of those blocks — creations which sometimes stand on their own, and sometimes, as with DALL-E, are themselves combined into even larger Lego superstructures.
Diffusion models such as DALL-E’s are generally structured as “U-Nets,” so named because when drawn they look like a U. The key feature of U-Nets is that they make heavy use of skip connections. Getting back to our waterfall analogy, in a U-Net, in addition to the standard one-layer-at-a-time flow, some of the data “water” might go directly from the third layer to the third last layer, some more from the sixth layer to the sixth last layer, and so forth.
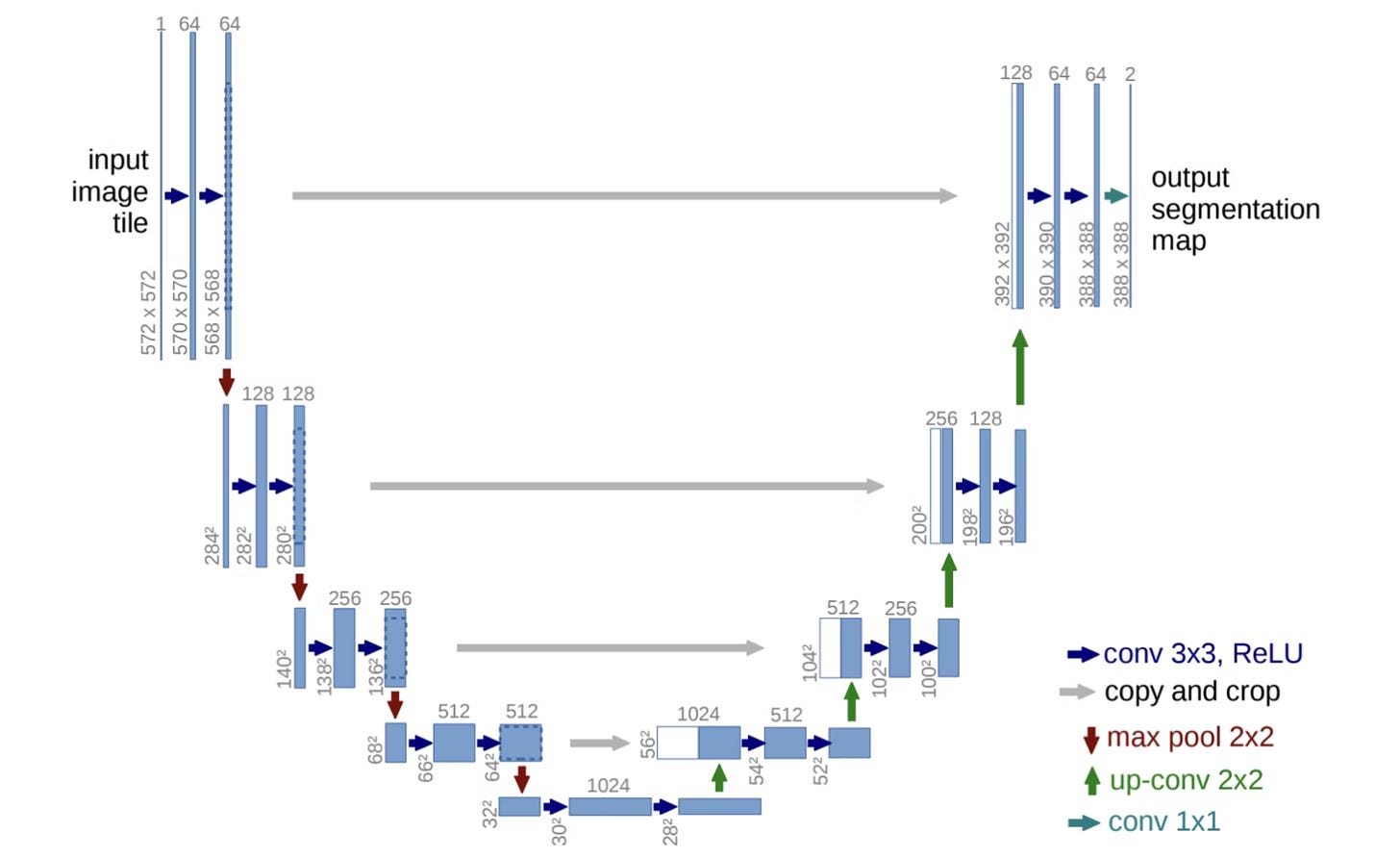
The fundamental advantage of a U-Net is that its inputs get deeply processed by every layer of the neural network, but are also passed directly to the later layers so they don’t get “watered down” by previous processing. It turns out that when the bottom layers can make simultaneous use of the direct inputs and their fully processed results, the resulting trained model is much more subtle and powerful.
But. There is always a but, as they say. All these interconnections mean even more training, and training is extremely expensive in terms of time, computing power, and therefore money. We don’t know how much DALL-E cost to train, but it was certainly well into the millions of dollars … and that’s with a trick they used to reduce the cost by probably 99%! That trick being: upsampling.
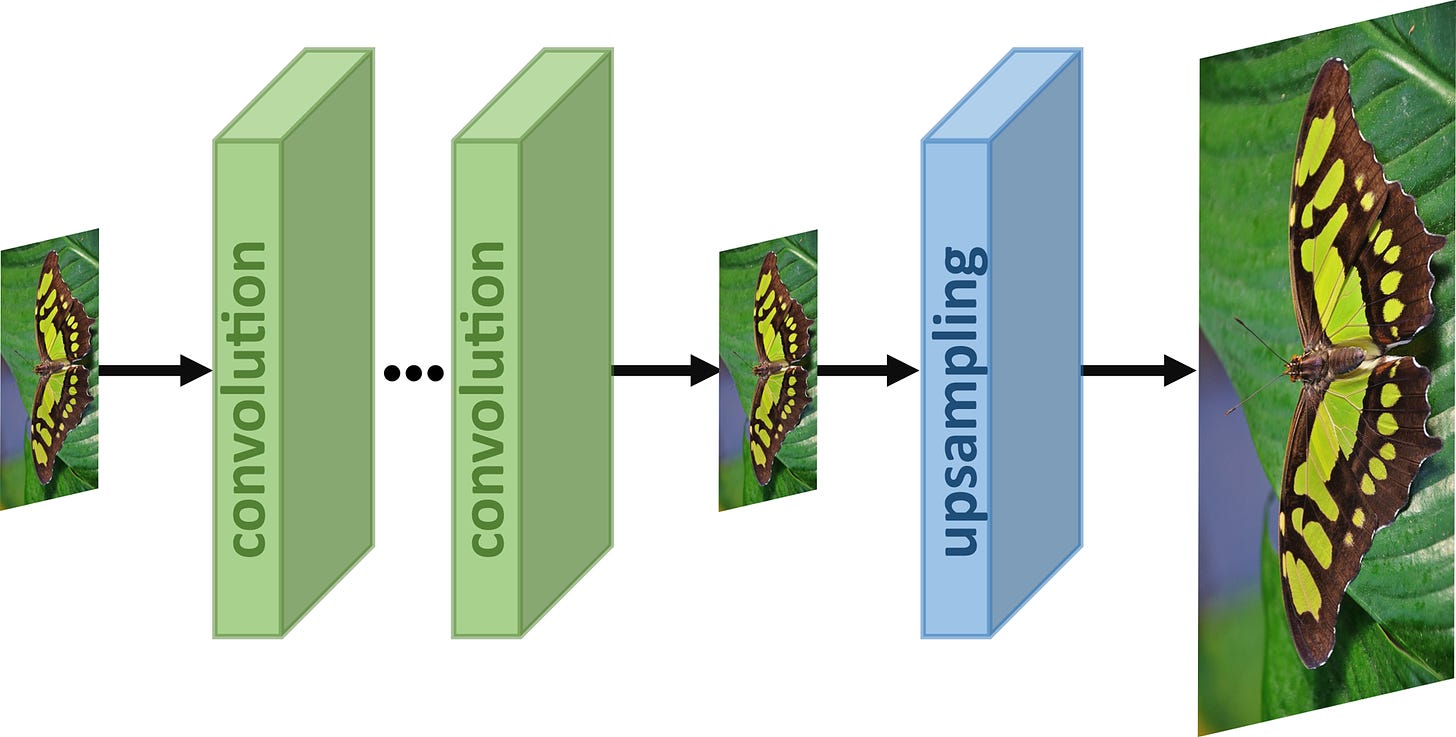
DALL-E generates full-sized 1024x1024 images. But in order to keep training time and cost semi reasonable, OpenAI hasn't trained DALL-E's core models to parse or generate images of that size. Instead, they use the diffusion model(s) to generate 64x64 images; and then “upsample” those to 1024x1024. That's 256 times larger! (OK, I know I promised there wouldn’t be math, but take my word for it, 1024x1024 really is 256 times as many pixels.) You may well wonder, if all the magic happens to 64x64 images, how can the 1024x1024 ones possibly be so good?
It’s worth noting that 64x64 is actually a pretty decent size for recognizable visual concepts. Thumbnails are often that size, and the human brain is pretty good at recognizing full-size images from thumbnails. In fact, we can go much smaller; I once saw an excellent exhibit at the Montreal Museum of Contemporary Art which was merely 16x16 monochromatic pixels, on which was displayed a “video” of people walking, and individual gaits were immediately recognizable despite that very limited size and color. Sadly that exhibit seems ungoogleable, but here’s something similar:

Still, the question remains: even if it's theoretically possible to downsample to 64x64 and keep an image's salient details and features, and then upsample all the way to 1024x1024 while maintaining the level of clarity and detail ... how?
By this point you'll be unsurprised to hear that the answer is -- that's right -- by adding even more neural networks to the chain. It turns out you can specifically train a diffusion model for “super-resolution,” i.e. upsampling. This should be unsurprising; if you fire up a photo editor on your computer and manually adjust the size of a 64x64 picture to 256x256, you’ll get what looks a whole lot like … a very noisy 256x256 picture! And what are diffusion models good at, again? Reducing noise. So DALL-E takes the 64x64 thumbnail, uses another diffusion model to expand it to 256x256 (sixteen times larger!) and then yet another diffusion model to expand it to 1024x1024 (sixteen times larger yet!) That’s right, DALL-E isn’t three neural networks but five; encoder, prior, decoder, upsampler, and second upsampler. It stops there, though, I swear.
vii. Putting it all together
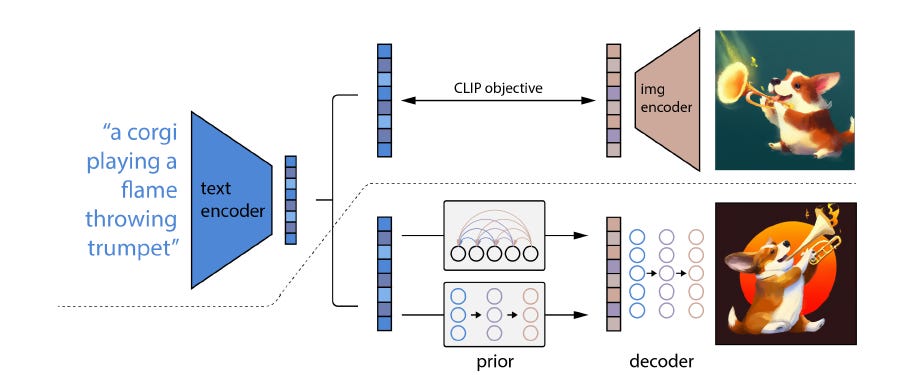
OK, let's talk about all of DALL-E, start to finish. Its input is your text prompt. Its output is the generated image. In between, it goes through a CLIP text encoder; a "prior" diffusion model that creates an image embedding, which you can think of as “a collection of visual features,” associated with that prompt; the diffusion model “decoder” where the image-generation magic and nudging happen; and, finally, two consecutive upsamplers, ballooning the image size from 64x64 to 1024x1024.
Of course DALL-E is far from the only prominent AI image generator. The others — Midjourney, Craiyon, Imagen, and above all the open-source run-it-on-your-own-computer Stable Diffusion — are also diffusion models, but all are architected subtly differently and have their own strengths, weaknesses, and idiosyncracies. For instance, DALL-E basically cannot spell, whereas Imagen is quite good at it.
Interestingly, even DALL-E’s creators don’t know why it can’t spell! They speculate it has to do with the way it encodes and embeds text — but as you can see, there’s still a substantial amount of “feel,” aka guesswork, when it comes to interpreting models’ peculiarities. I might write a future post about the differences and similarities between these generators … but I think you’ll agree this particular post is already long enough.
viii. TL;DR
Let's just itemize what I consider the key points:
I believe modern AI will be a world-transformative technology, so it's important that non-technical people understand it.
Neural networks are agglomerations of “neurons,” which receive a slew of inputs, assign a weight to each, and output a single corresponding value based on a simple mathematical function.
Neurons are generally arrayed in “layers” through which data passes. Their operation can be analogized to water flowing down a staircases; the data is the water, each stair is a layer.
Neural networks are trained by defining a mathematical function which describes the difference between their actual and desired output, and then using backpropagation to “walk back up" the layers, mathematically calculating which direction each weight needs to change, and tweaking it accordingly — until eventually, after many training runs, the actual and the desired (mostly) merge. Trained neural networks are often known as “models.”
DALL-E (like all diffusion models) is trained by showing it many pictures to which noise is slowly added, over a thousand or so steps, until they turn into random static. DALL-E then learns to estimate, when shown a noisy picture, what noise was added in the previous "noising" step. By subtracting that estimated noise, one step at a time — by "denoising" — it can start with noise and ultimately generate a brand-new, high-quality image.
By training DALL-E on captions as well as images, we teach it to “nudge” the generated image at every step towards one corresponding to the user’s text prompt. This correspondence is much improved by the use of a text encoder and “prior” diffusion model, to transform the user's text prompt into an optimal input,
Because models as effective as DALL-E are incredibly expensive to train, consuming enormous amounts of computing power, it is trained to generate relatively small 64x64 images, which are then upsampled to 1024x1024 pixels.
Architecting an effective network by stacking different kinds and types of neural layers together, and connecting trained models together to build a product or system, remains as much art form as science.
ix. Credits
All errors in the above are essentially certainly mine. If you spot any, kindly let me know, and I’ll endeavor to quickly note and correct them. Below is a list of the references which I found most helpful when writing this post:
“How diffusion models work: the math from scratch” by Sergios Karagiannakos and Nikolas Adaloglou
Which in turn seems to be largely based on the great Lilian Weng’s “What are diffusion models?”
“Introduction to Diffusion Models for Machine Learning” and “How DALL-E 2 Actually Works” by Ryan O’Connor
“The Annotated Diffusion Model” by Niels Rogge and Kashif Rasul
“Skip Connections” by Nikolas Adaloglou again
“Neural Networks and Deep Leaning” by Michael Nielsen, particularly chapter 2, “How the backpropagation algorithm works”
“Backpropagation” and “Gaussian noise” on Wikipedia
“OpenAI and the road to text-guided image generation” by Grigory Sapunov
“How Does DALL·E 2 Work?” by Aditya Singh
“OpenAI's DALL-E 2 and DALL-E 1 Explained” by Vaclav Kosar
“Generative Modeling by Estimating Gradients of the Data Distribution” by Yang Song
“From DALL·E to Stable Diffusion: how do text-to-image generation models work?” by Ian Spektor
“Latent Diffusion Models: The Architecture behind Stable Diffusion” by Louis Bouchard
“Deep Unsupervised Learning using Nonequilibrium Thermodynamics” by Jascha Sohl-Dickstein, Eric A. Weiss, Niru Maheswaranathan, and Surya Ganguli
“Image Super-Resolution via Iterative Refinement” by Chitwan Saharia, Jonathan Ho, William Chan, Tim Salimans, David J. Fleet, and Mohammad Norouzi
and of course “Hierarchical Text-Conditional Image Generation with CLIP Latents,” a.k.a. ‘the DALL-E 2 paper,’ by Aditya Ramesh, Prafulla Dhariwal, Alex Nichol, Casey Chu, and Mark Chen.







